Gleichungen lösen
Für jede selbständig gelöste Aufgabe bekommst du einen Punkt, für jeweils 50 Punkte einen Stern.
Aktueller Punktestand: 0
Hinweise zur Eingabe
- Notiere die Lösungen in der Reihenfolge der Faktoren
- Falls es keine Lösungen gibt, Felder leer lassen
- Notiere Hochzahlen mit dem Dach-Symbol: x^n
- x² = x^2
- x³ = x^3
Rechenregeln und Beispiele
Regeln:
- 1. Schritt: Alle Zahlen nach rechts bringen durch Addieren oder Subtrahieren beider Seiten der Gleichung mit der passenden Zahl.
- 2. Schritt: Alle Variablen x nach links bringen durch Addieren oder Subtrahieren beider Seiten der Gleichung mit dem passenden Term.
- 3. Schritt: Durch den Vorfaktor von x dividieren.
Beispiel 1:
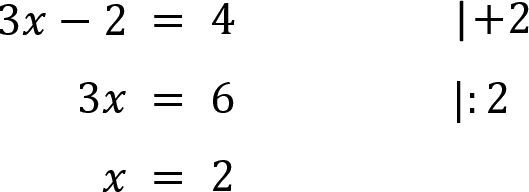
Beispiel 2:
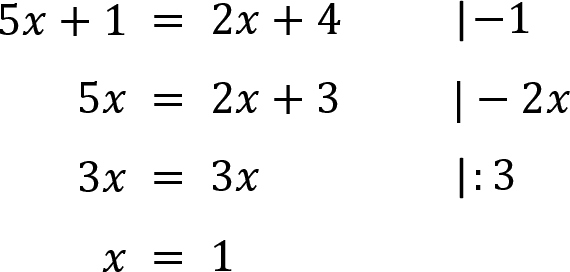
Regel:
- Das Produkt a⋅b zweier Zahlen ist 0, wenn a = 0 oder b = 0 gilt.
Beispiel:
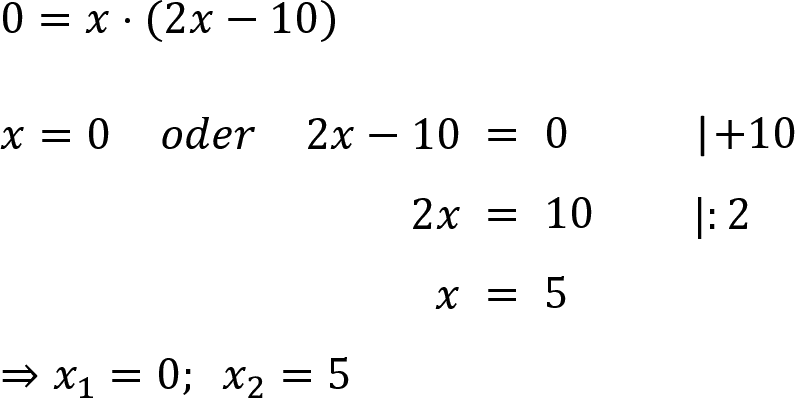
Regeln:
- Distributivgesetz "rückwärts": a ⋅ b + a ⋅ c = a ⋅ (b + c)
- Klammere immer die größtmögliche Zahl und x-Potenz aus!
- Wende anschließend den Satz vom Nullprodukt an.
Beispiel 1:
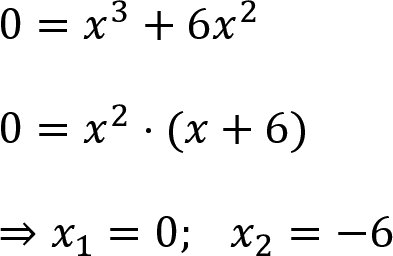
Beispiel 2:
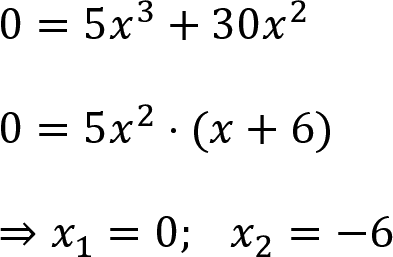
Regeln:
- 1. Schritt: Alle Zahlen nach rechts bringen durch Addieren oder Subtrahieren beider Seiten der Gleichung mit der passenden Zahl.
- 2. Schritt: Durch den Vorfaktor von x dividieren.
- 3. Schritt: Auf beiden Seiten die n-te Wurzel ziehen und Fallunterscheidung machen:
- Bei geraden Hochzahlen gibt es entweder zwei Lösungen oder keine Lösung (beide Felder leer lassen!)
- Bei ungeraden Hochzahlen gibt es immer eine Lösung (zweites Feld leer lassen!)
Beispiel 1:
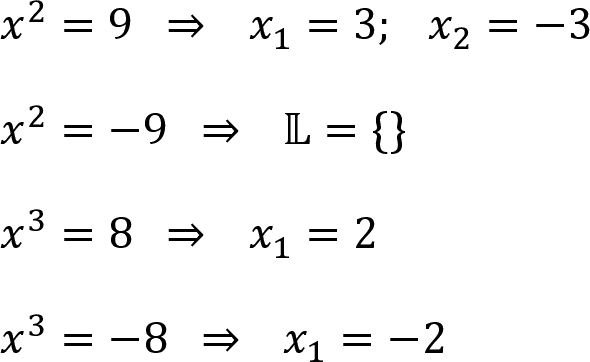
Beispiel 2:
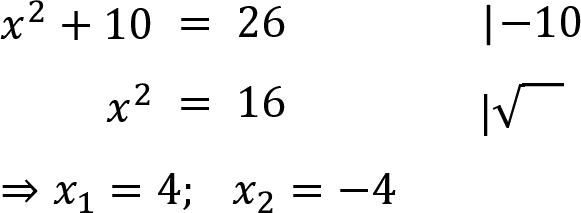
Regeln:
- Die Lösungen von quadratischen Gleichungen der Form ax² + bx + c =0 können mit der abc-Formel bestimmt werden:
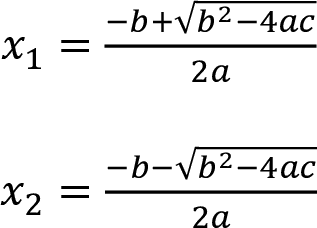
- Den Ausdruck unter der Wurzel nennt man Diskriminante D. Entsprechend kann man die Lösungen schrittweise berechnen:
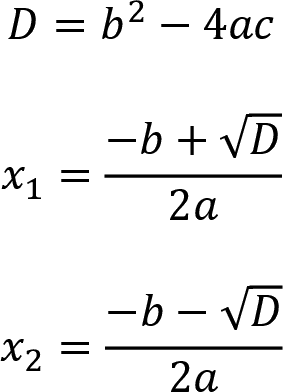
- Fallunterscheidung:
- Ist die Diskriminante D größer als Null, hat die Gleichung zwei Lösungen
- Ist die Diskriminanten D gleich Null, hat die Gleichung eine Lösung (zweites Feld leer lassen!)
- Ist die Diskriminante D kleiner Null, hat die Gleichung keine Lösung (beide Felder leer lassen!)
Beispiel:
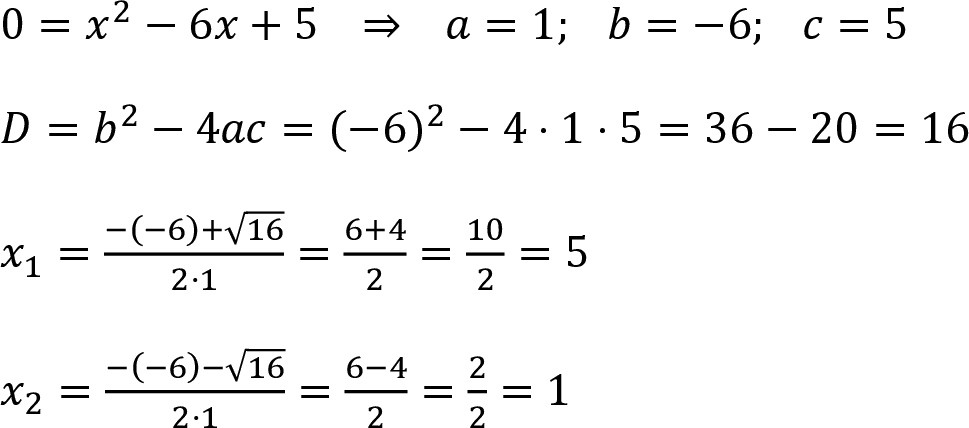
Programmierung: J. Merkert



