Graphen
Für jede selbständig gelöste Aufgabe bekommst du einen Punkt, für jeweils 50 Punkte einen Stern.
Aktueller Punktestand: 0
Hinweise zur Eingabe
- Notiere die Steigung ggf. als Bruch in Divisionsschreibweise, Verschiebungen aber als Kommzahlen:
- f(x) = 1/2 * x - 3,5
- f(x) = -1/4 * x + 1,5
- Notiere Hochzahlen mit dem Dach-Symbol: x^n
- x² = x^2
- x³ = x^3
Rechenregeln und Beispiele
Funktionsgleichung: f(x) = m ⋅ x
- m: Steigung
- Bestimmung mit Hilfe des Steigungsdreiecks Δy/Δx
Beispiele:
- f(x)= 2 ⋅ x
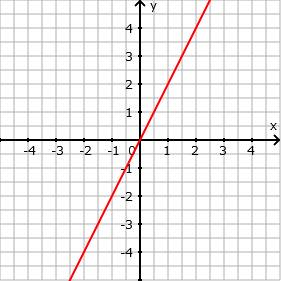
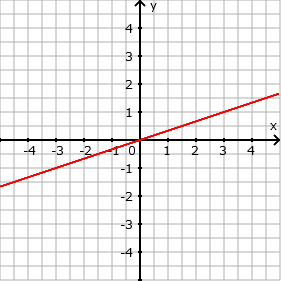
- f(x)= 1/3 ⋅ x
- Eingabe: 1/3 * x
Funktionsgleichung: f(x) = m ⋅ x + c
- m: Steigung
- Bestimmung mit Hilfe des Steigungsdreiecks Δy/Δx
- c: y-Achsenabschnitt
Beispiele:
- f(x)= -2x + 4
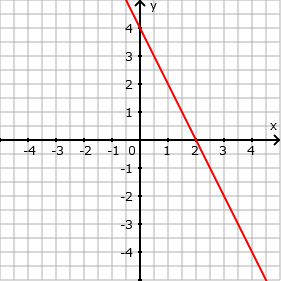
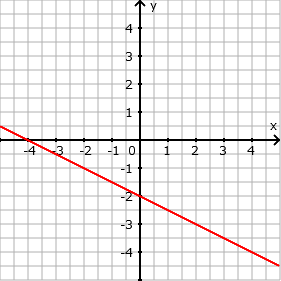
- f(x)= -1/2 x - 2
- Eingabe: -1/2 * x - 2
Regeln:
- Verschiebung um c in y-Richtung nach oben: f(x) = g(x) + c
- Verschiebung um b in x-Richtung nach rechts: f(x) = g(x - b)
- Streckung in y-Richtung mit Streckfaktor a: f(x) = a ⋅ g(x)
- Sonderfall: Spiegelung an der x-Achse: f(x) = - g(x)
Beispiele:
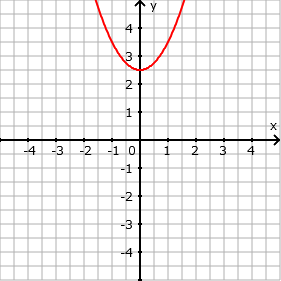
- Verschiebung um 2,5 in y-Richtung nach oben: f(x) = x² + 2,5
- Eingabe: x^2 + 2,5
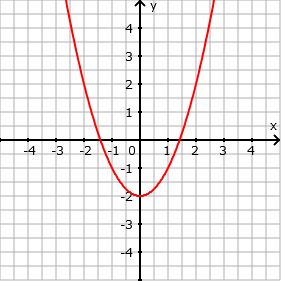
- Verschiebung um 2 in y-Richtung nach unten: f(x) = x² - 2
- Eingabe: x^2 - 2
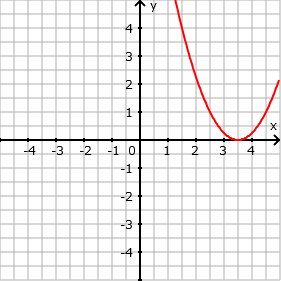
- Verschiebung um 3,5 in y-Richtung nach rechts: f(x) = (x - 3,5)²
- Eingabe: (x - 3,5)^2
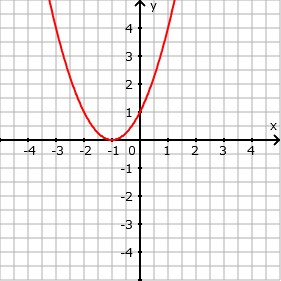
- Verschiebung um 1 in y-Richtung nach links: f(x) = (x + 1)²
- Eingabe: (x + 1)^2
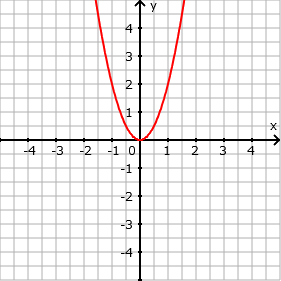
- Streckung in y-Richtung mit Streckfaktor 2: f(x) = 2 x²
- Eingabe: 2x^2
- Beachte den y-Wert bei x = 1: f(1) = 2 ⋅ 1² = 2!
Regeln:
- Verschiebung um c in y-Richtung nach oben: f(x) = g(x) + c
- Verschiebung um b in x-Richtung nach rechts: f(x) = g(x - b)
- Streckung in y-Richtung mit Streckfaktor a: f(x) = a ⋅ g(x)
- Sonderfall: Spiegelung an der x-Achse: f(x) = - g(x)
Beispiele:
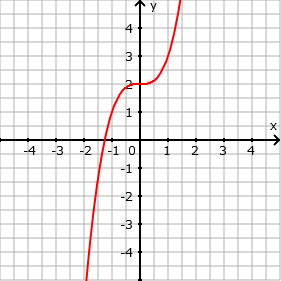
- Verschiebung um 2 in y-Richtung nach oben: f(x) = x³ + 2
- Eingabe: x^3 + 2
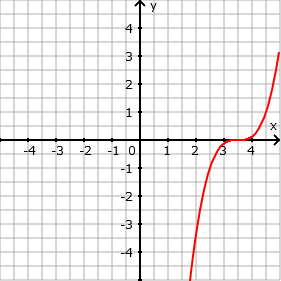
- Verschiebung um 3,5 in y-Richtung nach rechts: f(x) = (x - 3,5)³
- Eingabe: (x - 3,5)^3
Regeln:
- Verschiebung um c in y-Richtung nach oben: f(x) = g(x) + c
- Verschiebung um b in x-Richtung nach rechts: f(x) = g(x - b)
- Streckung in y-Richtung mit Streckfaktor a: f(x) = a ⋅ g(x)
- Sonderfall: Spiegelung an der x-Achse: f(x) = - g(x)
Beispiele:
- Verschiebung um 3 in y-Richtung nach unten: f(x) = 1/x - 3
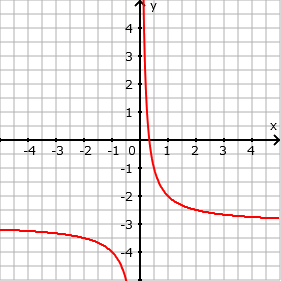
- Verschiebung um 3 in y-Richtung nach rechts: f(x) = 1/(x-3)
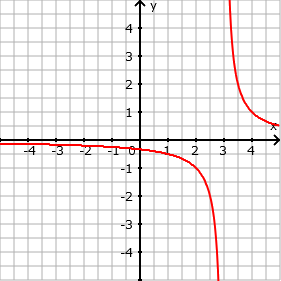
- Verschiebung um 2 in y-Richtung nach links: f(x) = 1/(x+2)
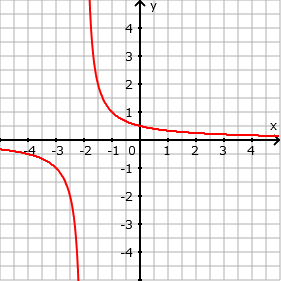
Allgemeine Funktionsgleichung: f(x) = a ⋅ sin[b ⋅ (x - c)] + d
- Streckung mit Faktor a (= Amplitude) in y-Richtung
- Streckung mit Faktor 1/b (!) in x-Richtung
- Die Zahl b lässt sich aus der Periode p mit der Formel b = 2π / p berechnen.
- Umgekehrt kann man die Periode p aus der Zahl b mit der Formel p = 2π / b berechnen.
- Verschiebung um c in x-Richtung nach rechts
- Die Verschiebung in x-Richtung ist nicht eindeutig ablesbar, da zu c beliebige Vielfache der Periode p addiert werden können. Deshalb kommen bei dieser Online-Übung nur Funktionen der Form f(x) = a ⋅ sin(b ⋅ x) + d vor.
- Verschiebung um d in y-Richtung nach oben
Beispiele:
- Streckung mit Faktor 2,5 in y-Richtung (d.h. Amplitude a = 2,5): f(x) = 2,5 sin(x)
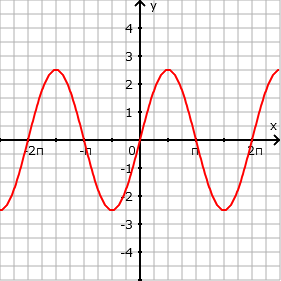
- Verschiebung um 1,5 in y-Richtung nach oben: f(x) = sin(x) + 1,5
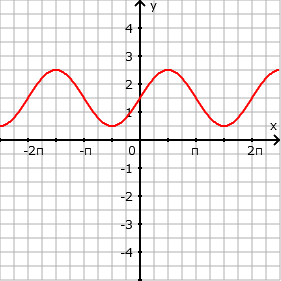
- Streckung mit Faktor 2 in x-Richtung: b = 1/2 und damit f(x) = sin(1/2 ⋅ x)
- Eingabe als Bruch: sin(1/2 * x)
- Die Periode hat sich von p = 2π auf p = 4π verdoppelt
- Rechnung mit Formel: p = 2π / b = 2π / (1/2) = 4π
Programmierung: J. Merkert



